线性回归算法评估指标MSE、RMSE、MAE、R方
如何评价一个线性回归模型的好坏,常见的评价指标有四种,均方误差(Mean Squared Error)、均方根误差(Root Mean Squared Error)、平均绝对值误差(Mean Absolute Error)以及R Squared。
均方误差(MSE)
实际值减预测值的平方和除以预测样本大小,使得其与测试样本大小无关。
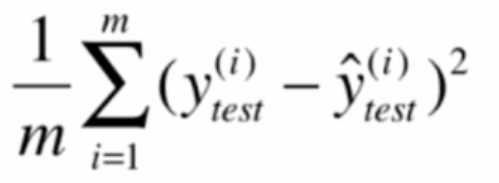
1 | mean_squared_error = np.sum((y_true-y_predict)**2) / len(y_predict) |
均方根误差(RMSE)
我们对式子加了一个平方。但这可能会导致量纲的问题,如房子价格为万元,平方后就成了万元的平方,对MSE开方,使量纲相同。
RMSE值越小,模型的预测性能越好。
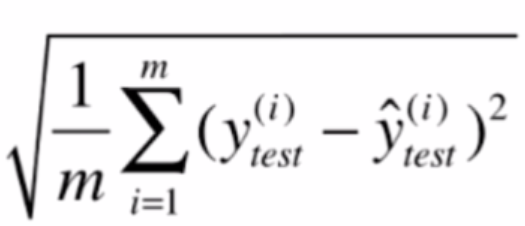
1 | root_mean_squared_error = sqrt(mean_squared_error) |
平均绝对值误差(MAE)
MSE与RMSE的区别仅在于对量纲是否敏感,因此又得出新方法,通过加绝对值,量纲相同。
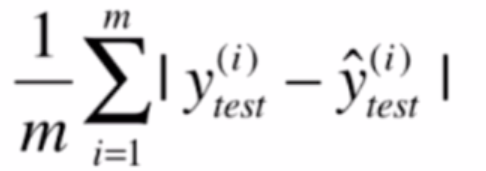
1 | mean_absolute_error = np.sum(np.absolute(y_true - y_predict)) / len(y_true) |
R方(R Squared)
对于上述的衡量方法,如RMSE和MAE还是有问题的,还是因为量纲不一样。比如我们预测考试分数误差是10,预测房价误差是1w。但我们却不能评价我们的模型是更适合预测分数还是预测房价。
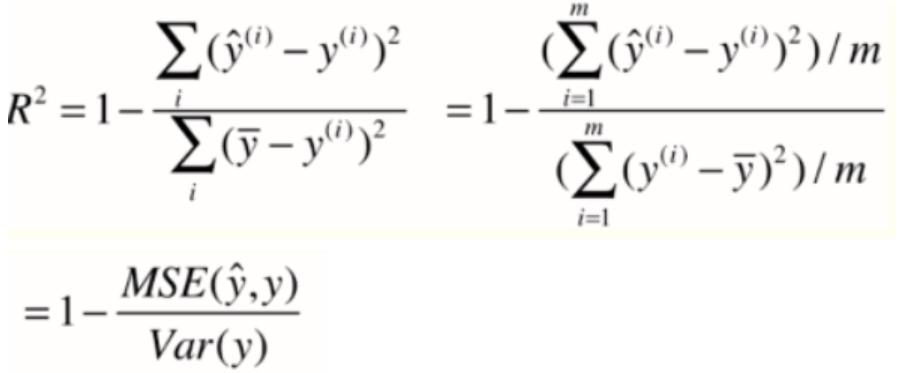
R2<=1,R2越大预测模型越好,最大值为1,当R2为0时预测模型等于基准模型,当R2<0时说明预测模型还不如基准模型,也可能数据不存在线性关系。
1 | r_squared = 1 - mean_squared_error / np.var(y_true) |


