概率论

第二章 随机变量及其分布

本章主要掌握概率分布函数与概率密度之间的转换

随机变量

定义：随实验结果而变的量X称为随机变量

常见的两类随机变量：离散型、连续型

离散型随机变量及其分布

定义：取值可数的随机变量为离散量

三个主要的离散型随机变量

0-1分布

X	0	1
P	q	p

p+q=1

二项分布

n重贝努利试验：设实验E只有两种可能的结果：A, 非A，P（A）=p，0<p<1,将E独立重复进行n次，则称这一串重复的独立实验为n重贝努利试验。

即：每次实验结果互不影响，在相同条件下重复进行

eg：独立重复抛n次硬币

设A在n重贝努利试验中发生X次，则：

$$P(X=k)=C_{n}^{k}p_{k}^{k}(1-p)^{n-k}, k=0,1, \ldots, \quad n$$

并称X服从参数为p的二项分布，记 X~ b(n,p)

泊松分布（Poisson分布）

若随机变量X的概率分布律为：

$$P(X=k)=\frac{e^{-\lambda} \lambda^{k}}{k !}, k=0,1,2, \cdots, \lambda>0$$

称X服从参数为λ的泊松分布，记 X~Π（λ）

随机变量的分布函数

定义：随机变量X，对任意实数x，称函数F（x）=P（X≤x）为X的概率分布函数，简称分布函数。

几何意义：

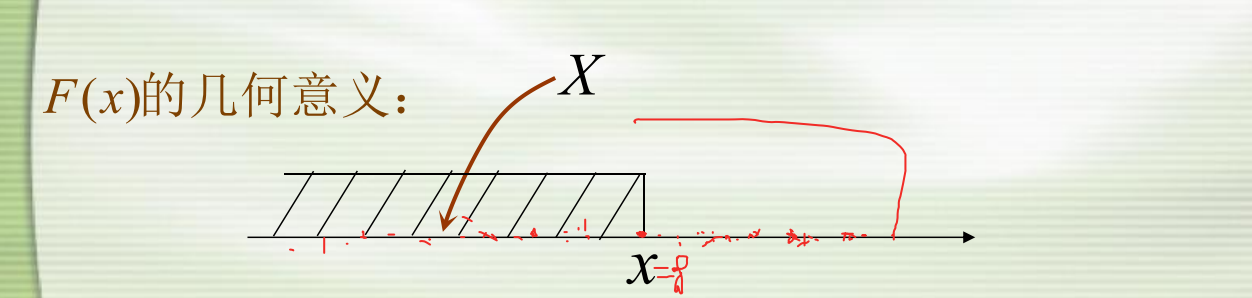
F（x）的性质：（1）0≤F（x）≤1

​ （2）F（x）单调递增，且F（-∞）=0，F（+∞）=1

连续型随机变量极其概率密度

定义：对于随机变量X的分布函数F（x），若存在非负函数f（x），使对于任意实数x，有：

$$F(x)=\int_{-\infty}^{x} f(t) d t$$

则称X为连续型随机变量，其中f（x）称为X的概率密度函数，简称概率密度。

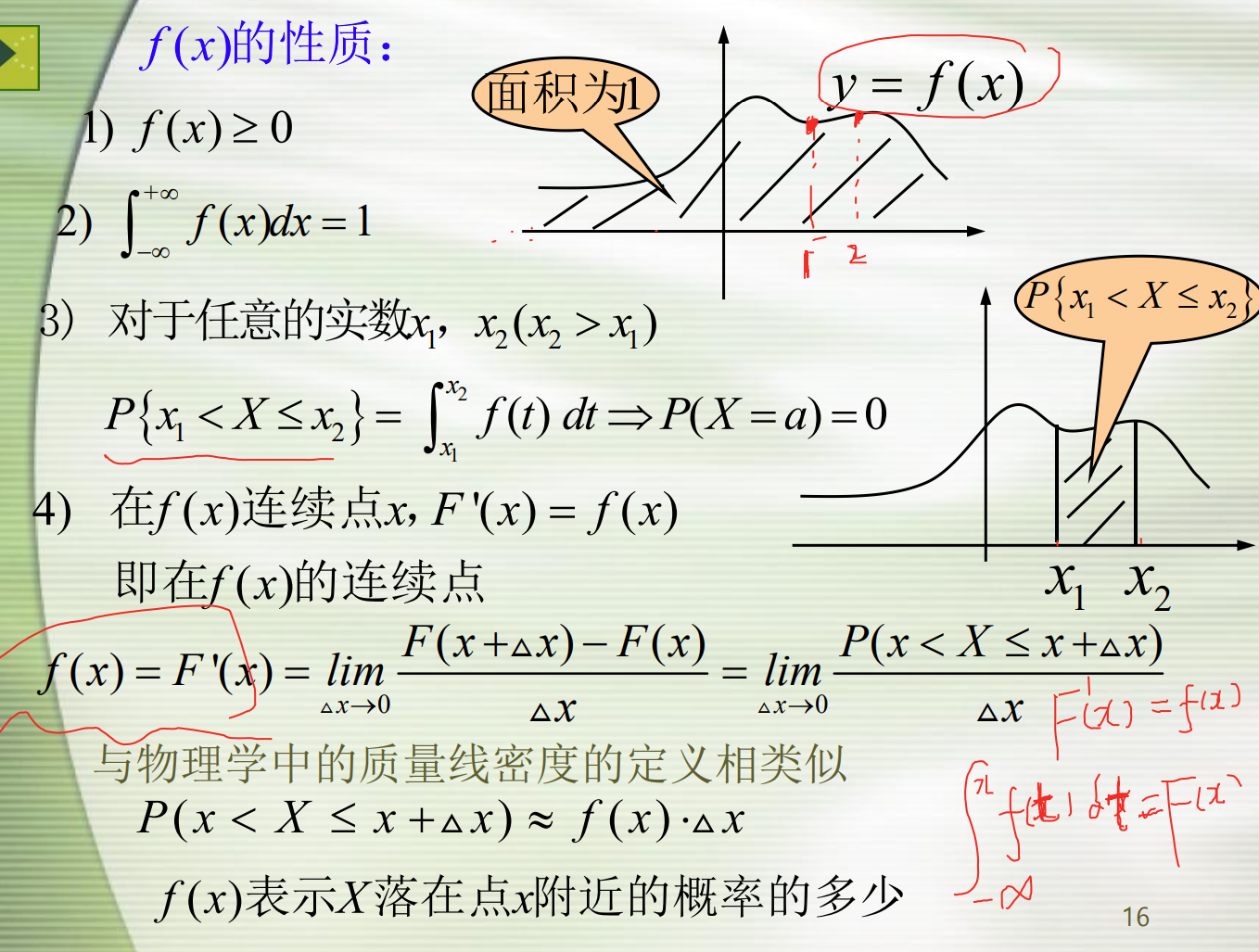
🔺 概率密度求积分为分布函数，概率分布函数求导为概率密度

几种重要的连续性随机变量

均匀分布

定义：X具有概率密度：

$$f(x)=\left\{\begin{array}{ll} \frac{1}{b-a} & x \in(a, b) \\ 0 & \text { 其他 } \end{array}\right.$$

称X在区间（a,b）上服从均匀分布，记为X~U（a,b）

指数分布

定义：设X的概率密度为：

$$f(x)=\left\{\begin{array}{ll} \lambda e^{-\lambda x} & x>0 \\ 0 & x \leq 0 \end{array}\right.$$

其中λ>0为常数，则称X服从参数为λ的指数分布。记为：X~EP（λ）

分布函数：

$$F(x)=\left\{\begin{array}{ll} 1-e^{-\lambda x} & x>0 \\ 0 & x \leq 0 \end{array}\right.$$

正态分布

定义：设X的概率密度为：

$$f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{\frac{(x-\mu)^{2}}{2 \sigma^{2}}}$$

其中μ和σ方为常数，

则称X服从参数为μ和σ方的正态分布（gauss分布）

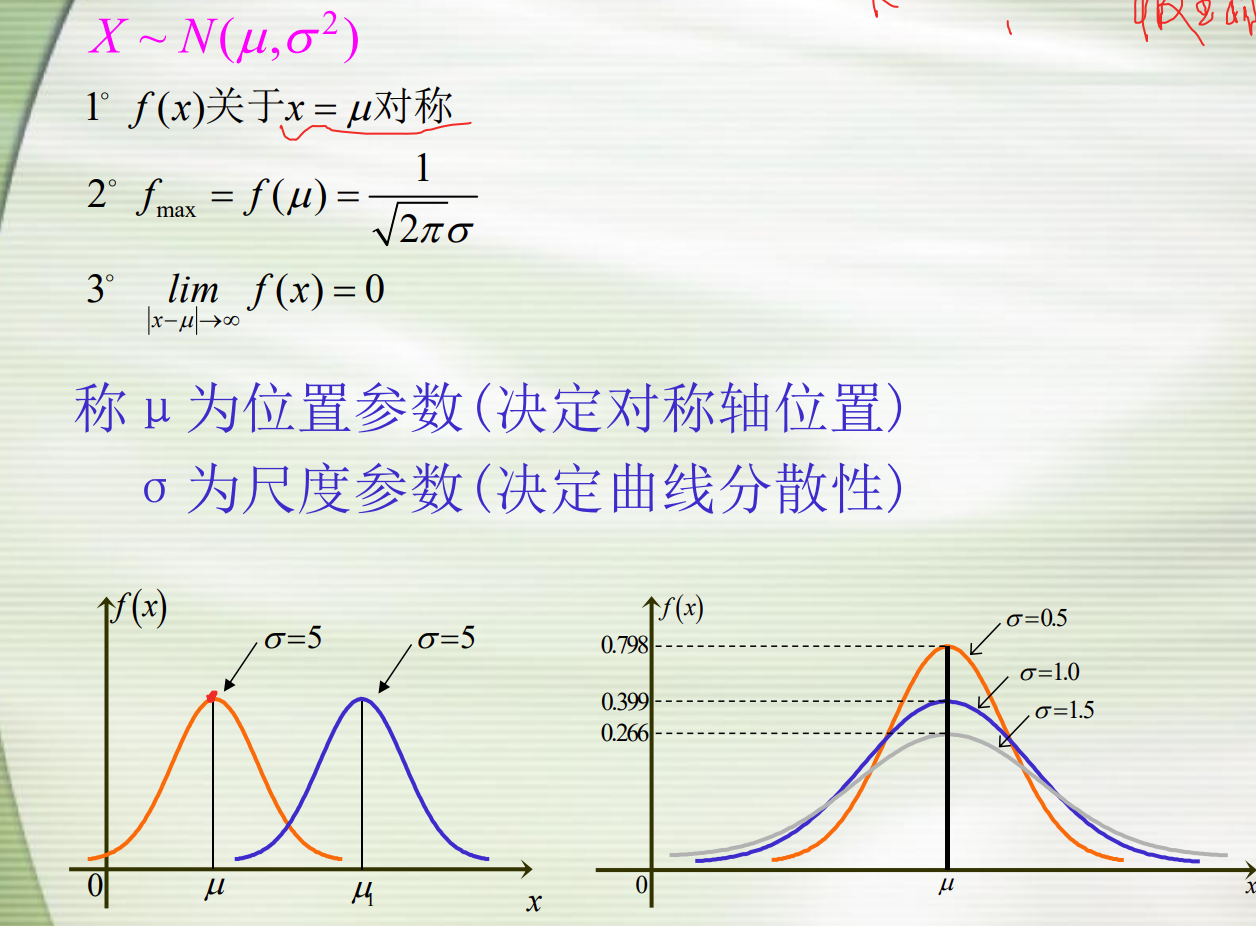
记为X~N（μ，σ^2）

同时有：

$$\int_{-\infty}^{+\infty} f(x) d x=1$$

随机变量的函数分布

第三章 多为随机变量及其分布

二维随机变量

定义

​ 定义：设E是一个随机试验，样本空间S={e}；设X=X(e)和Y=Y(e)是定义在S上的随机变量，由它们构成的向量(X,Y)叫做二维随机向量或二维随机变量。

​ 定义：设(X,Y)是二维随机变量对于任意实数x,y，二元函数 F(x,y) = P{(X≤x)∩(Y≤y)} == P(X≤x,Y≤y)称为二维随机变量(X,Y)的分布函数。

分布函数的性质

分布律的性质

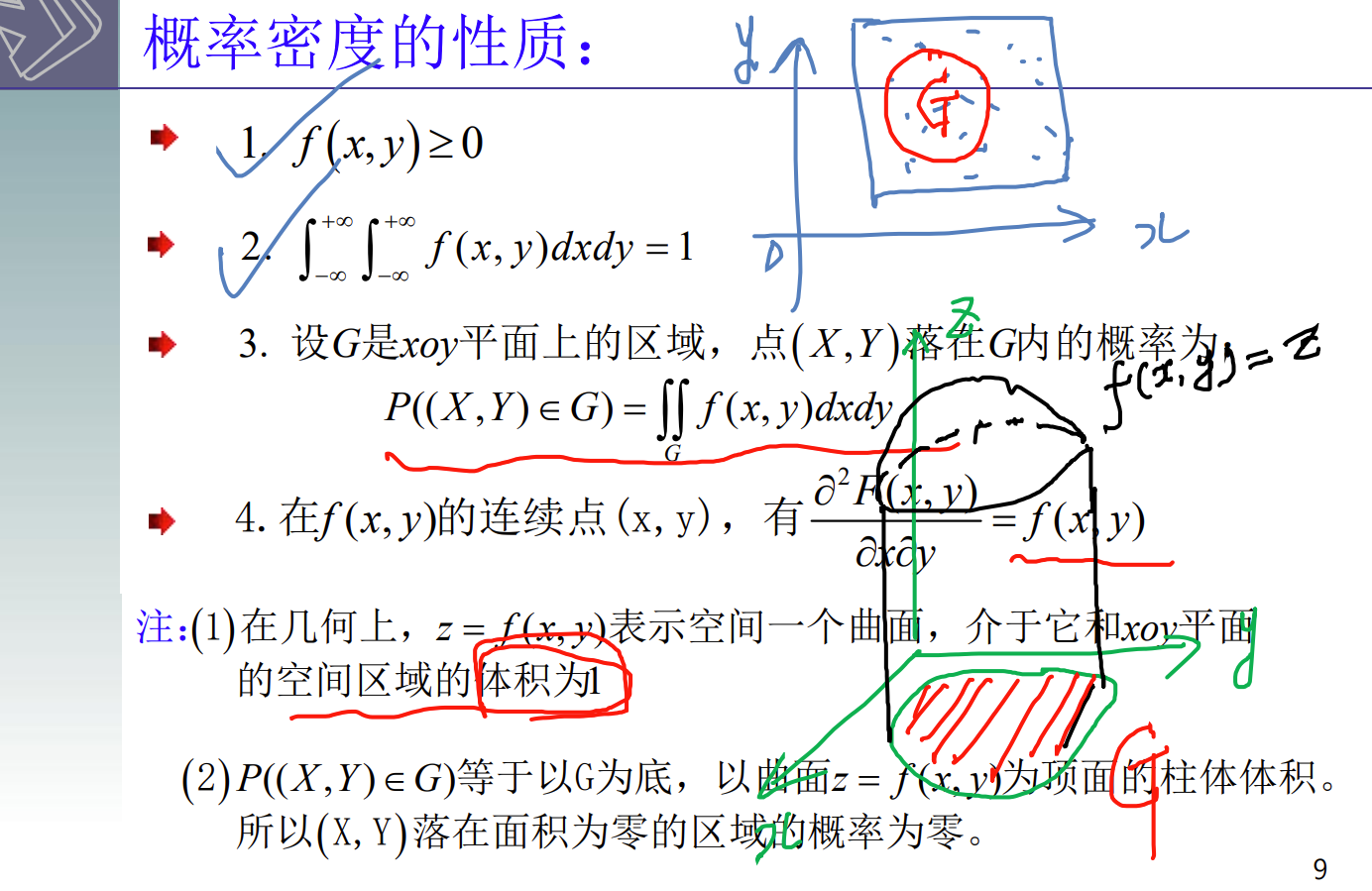
概率密度的性质