Logistic回归

线性回归与逻辑回归

​ 线性回归的模型是求出特征向量Y与输入样本矩阵X之间的线性关系系数θ，满足Y = Xθ。此时Y是连续的，所以是回归模型。

​ 如果我们想要Y离散，这时就需要对Y做一次变换，变成g（Y）。令g（Y）在某个实数区间是类别A，在另一个实数区间是类别B，以此类推，得到一个分类模型。

二元逻辑回归模型

​ 如果上述分类的类别只有两种，我们成为二元逻辑回归。对线性回归的结果用函数g进行转换，可以变化为逻辑回归。这个函数g在逻辑回归中我们一般使用sigmoid函数，函数形式如下：

$$g(z) = 1/(1+e^{-z})$$

sigmoid函数的图像如下：

​ 令g(z)中的z变为：z=xθ，这样就得到二元逻辑回归模型的一般形式：

$$h_{θ}（x）=1/（1+e^{-xθ}）$$

​ 其中x为样本输入，h为模型输出，可以理解为某一分类的概率大小。

​ 对于模型输出h(x)，如果h(x)>0.5，即xθ>0,则y=1；反之，y=0.y=0.5。

​ h(x)越小，分类为0的概率越高，反之，值越大分类为1的概率越高。

决策边界（Decision boundary）

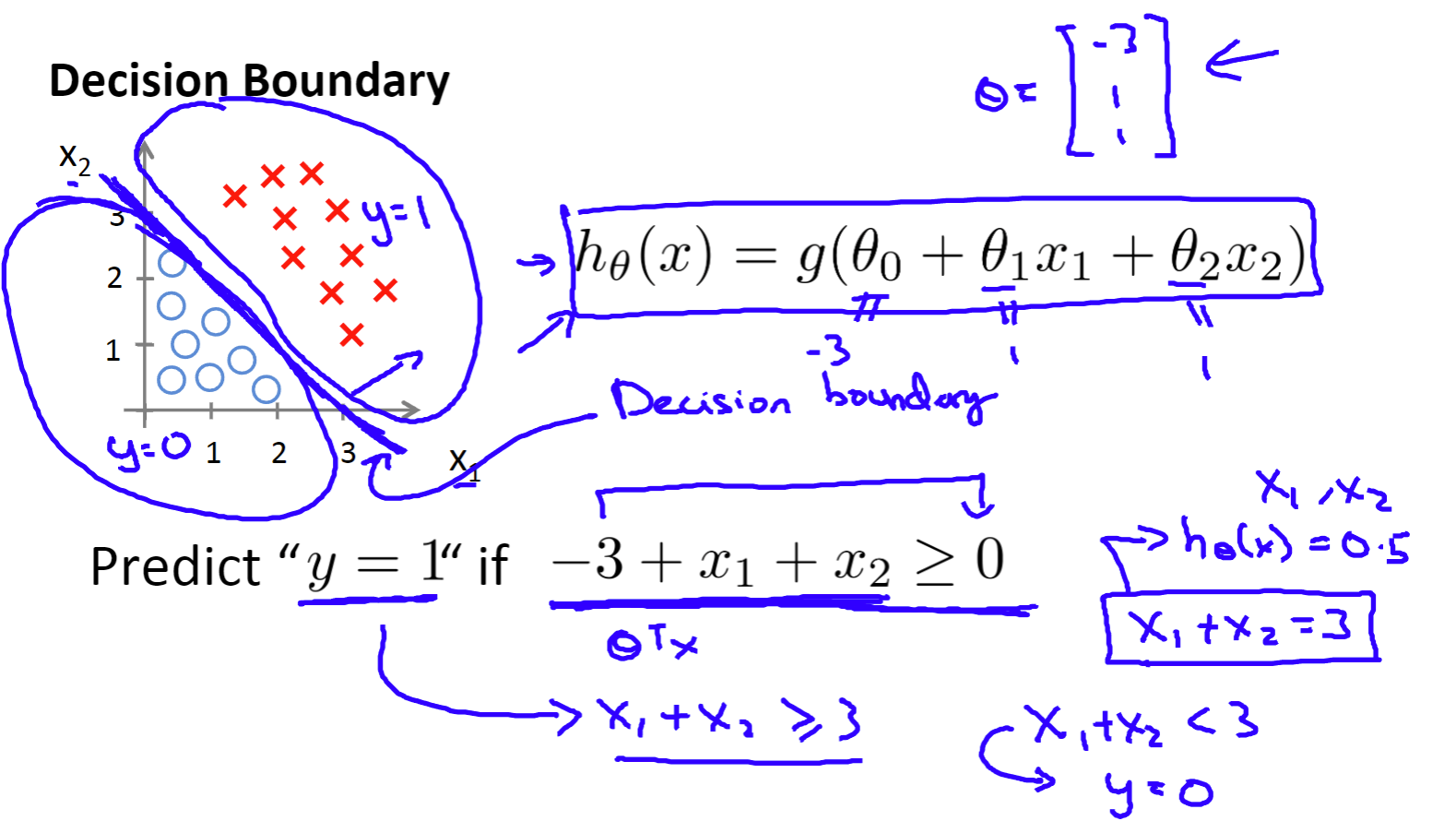
​ 如图，在设置出θ的值之后，我们便可以得出一条分界线，这条线便是决策边界

损失函数(Loss function)

​ 由于线性回归是连续的，所以可以使用模型误差的平方来定义损失函数。但是逻辑回归不是连续的，自然线性回归损失函数定义的经验就用不上了。

​ 假设我们的样本输出只有0和1两类，那么：

$$\begin{aligned} &P(y=1 \mid x, \theta)=h_\theta(x) \\ &P(y=0 \mid x, \theta)=1-h_\theta(x) \end{aligned}$$

这两个式子我们可以合成一个：

$$P(y \mid x, \theta)=h_\theta(x)^y\left(1-h_\theta(x)\right)^{1-y}$$

其中y只能为0或1.

通过极大似然估计法得到loss function：

$$J(\theta)=-\ln L(\theta)=-\sum_{i=1}^{m}\left(y^{(i)} \log \left(h_{\theta}\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right)$$