卷积

卷积的概念

所谓卷积，就是一个函数和另一个函数在某个维度上的加权”叠加“作用。

通俗的讲，卷积就是功能的叠加作用。举例来说，在一根铁丝某处不停弯曲，假设发热函数是f(t),散热函数是g(t)，此时此刻的温度就是f(t)跟g(t)的卷积。同理，记忆也是一种卷积的结果，假设认知函数是f(t)，代表对已有事物的理解，遗忘函数是g(t)，那么人脑中记忆函数h(t)就是f(t)与g(t)的卷积。

CV（Computer Version）中的卷积

计算机中的图像

在图像处理中应用卷积操作主要目的是利用特征模板对原始图像进行滤波操作，从而达到提取特征的目的。卷积可以很方便地通过从输入的一小块数据矩阵中学到图像的特征，并能保留像素间的相对空间关系。

卷积核

在卷积神经网络中通过一个方形矩阵（matrix）去扫描整张图像，图像中的所有像素点会被线性变换组合，形成下一层的神经元节点。这个”小方块“便是卷积核。下图为卷积操作实例。

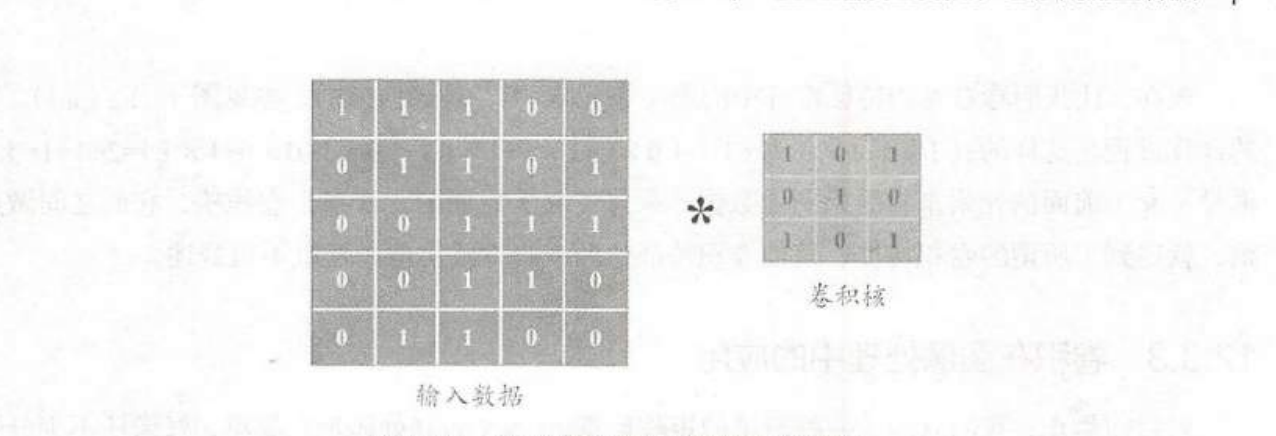
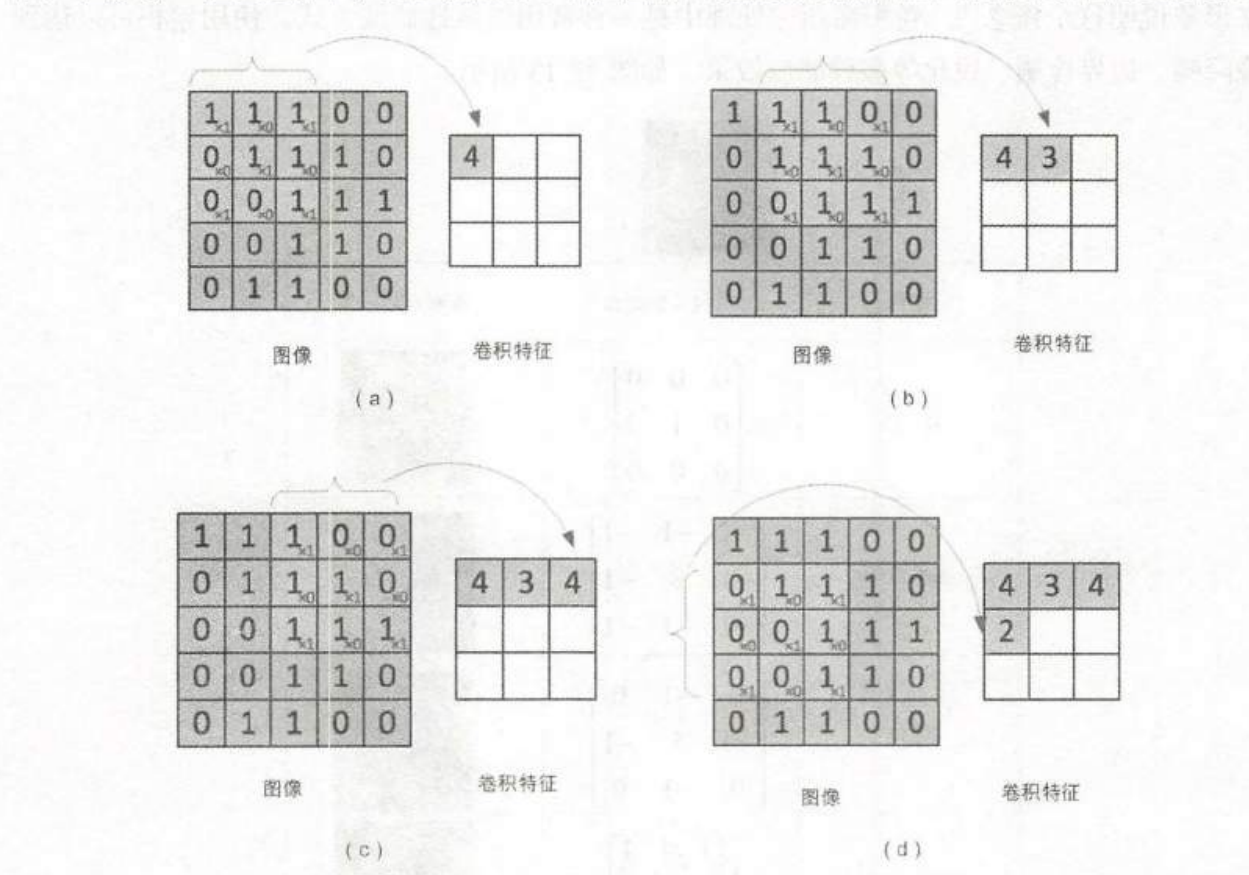
像这样从左到右、从上到下滑动，每次滑动s个像素，s称为“步幅”。以此类推，得到一个特征图谱（卷积特征）矩阵。

卷积神经网络的结构

一个典型的卷积神经网络通常有若干个卷积层(Convolutional Layer)、激活层(Activation Layer)、池化层以及全连接层(Fully Connected Layer)

卷积层

卷积神经网络的核心。在卷积层中，通过实现“局部感知”和“参数共享”，可以达到降维和特征提取。

激活层

激活层的作用是将前一层的线性输出通过激活函数进行处理，用来模拟任意函数，从而增强网络表征能力。深度学习中常用ReLU当作激活函数，因为它收敛更快，同时部分解决了梯度消失问题。（梯度消失：我们嵌套的多层卷积层，如果每个算出的值都是十分接近于0的数，在不断的链式乘积之后，就会变得更小，导致梯度消失）

池化层

也称子采样层或下采样层，这一层通过使用MaxPooling、Mean Poiling等方法，来实现数据规模的降低。巧妙的采样还具备局部线性转换不变性，从而增强卷积神经网络的泛化处理能力。

全连接层

这个网络层相当于多层感知机（MLP），其在整个卷积神经网络中起到分类器的作用。通过前面的多个“卷积-激活-池化”层的反复处理，待处理的数据特性已有了显著提高。

可以先由m个卷积层和激活层叠加，然后可以进行一次池化操作，重复这个结构n次，最后叠加k个全连接层。

Flatten

flatten是把feature map拉直，然后丢到全连接层(fully connected feedforward network),然后结束。

通过前面的层层堆叠，将输入层导入的原始数据逐层抽象，形成高层语义信息，送到全连接层做分类，这一过程便是“前馈运算”（Feed-forward）。最终通过计算输出值和预期值之间的差异，得到loss，然后再通过BP算法（反向传播），将误差逐层向后反馈（Back-forward），从而更新网络连接的权值。这样多次“前馈计算”“反馈更新”，知道模型收敛（loss小于给定的值）。这样一个CNN模型就训练完成了。